big o notation

what is it?

the language we use for talking about how long an algorithm takes to run (time complexity) or how much memory is used by an algorithm (space complexity)

for time complexity, the worst-case - what are the most operations/steps that could happen for an input of size n

Some types

O(1) → Constant Time

O(1) means that it takes a constant time to run an algorithm, regardless of the size of the input

examples

• math operations
• accessing an array via the index
• accessing a hash via the key
• pushing and popping on a stack
• insertion and removal from a queue
• returning a value from a function

O(n) → Linear Time

O(n) means that the run-time increases at the same pace as the input

examples

• traversing an array
• find in an array is also O(n), because for the worst case (at the end of the array for an unoptimized find) the time will linearly increase

O(n²) → Quadratic Time

O(n²) means that the calculation runs in quadratic time, which is the squared size of the input data

examples

• bubble sort
• insertion sort
• selection sort

generally speaking (but not always), seeing two nested loops is typically a good indicator that the piece of code you’re looking at has a run time of O(n²)

O(log n) → Logarithmic Time

O(log n) means that the running time grows in proportion to the logarithm of the input size. this means that the run time barely increases as you exponentially increase the input

examples

• binary search

O(n log n) → Linearithmic Time

between O(n) and O(n²)

examples

• merge sort
• timsort
• heapsort

Cheatsheet

link

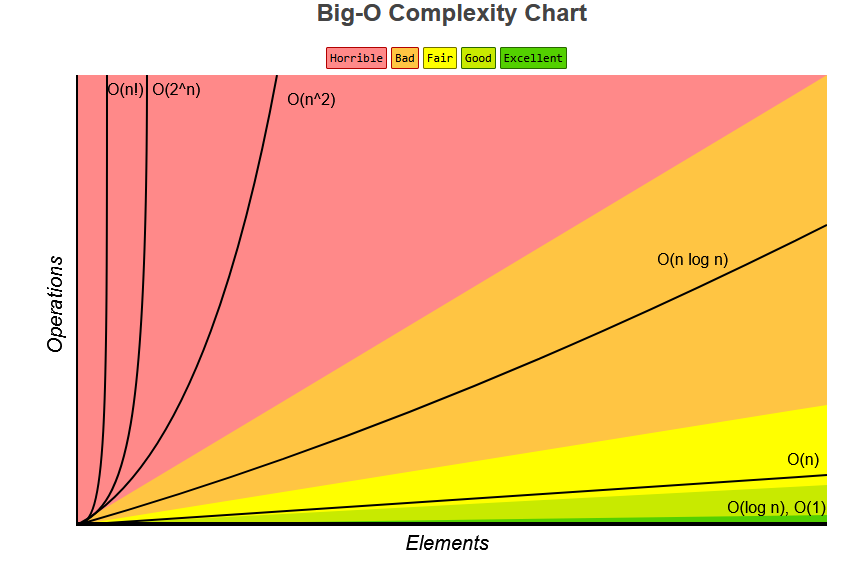
Calculating Big O

drop constants

def dummy(items):
    for i in range(len(items)): # O(n)
        print(items[i])         # O(1)
    
    for i in range(len(items)): # O(n)
        print(items[i])         # O(1)

remove the constants(O(1)) resulting in O(2n), then drop the 2, resulting in O(n)

drop non-dominant terms

def dummy(items):
    for i in range(len(items)):     # O(n)
        for j in range(len(items)): # O(n)
            print(items[i])         # O(1)
    
    for i in range(len(items)): # O(n)
        print(items[i])         # O(1)

results in O(n² + n) which can be simplified to O(n²)